 |
|
|
 |
|
|
An interesting problem to think about when looking at the above photograph
is "How can the car drive with an elliptical wheel?
Shouldn't wheels be circular?" Well, actually the wheels on the
car were circular. There are two reasons that it looks elliptical
in
the photograph:
(1) the camera used a focal-plane
shutter
(2) the car was moving.
The photograph was taken during the 1912 French Grand Prix by Jacques-Henri Lartigues.
Most modern cameras use a diaphragm shutter just behind the lens. A small diaphram opens up and then shuts exposing the film for just the right amount of time. Lartigues's camera, however, used a focal-plane shutter. It consisted of a narrow slit in an opaque sheet. The sheet was placed just atop the film in the "focal plane" of the camera and was drawn over the film rapidly. As the opaque sheet moved the slit exposed different portions of the image as it traveled across the film.
This explains the elliptical appearance of the circular wheel. The bottom part of the picture was exposed first. By the time the slit reached the part of the image with the top part of the wheel the car had already moved slightly forward. In fact we can tell by the way the people and poles in the background tilt to the right that Lartigues moved the camera ("panning") to try and follow the car. The bottom of the people were exposed first and the top of the people were exposed after the camera had moved.
What we see all at once in the picture was actually exposed at different times. "Simultaneous" for us viewing the photo is not the same as "simultaneous" in how the film was exposed. This together with the movement of the car gives it a funny, "different" shape in the photograph.]
This is exactly what happens in Special Relativity. Differing measurements of simultaneity lead to different measurements in the lengths of things. It all depends on which frame the measurements are taken in. In fact if the camera had been tilted 90 degrees so that the front of the car was exposed first and the rear part of the car exposed later then the photo would show a "length-contracted" car. Exactly what happens in relativistic length contraction.
Lets see this at work with the camera turned 90 degrees:
Here is our car driving along with speed v. The rectangle above the car is the film. The long "slit" at the right represents the slit in the focal plane shutter that will sweep across the film (the large rectangle). This will expose the corresponding parts of the car onto the film. The first image shows the front of the moving car about to be exposed by the focal-plane shutter onto the film
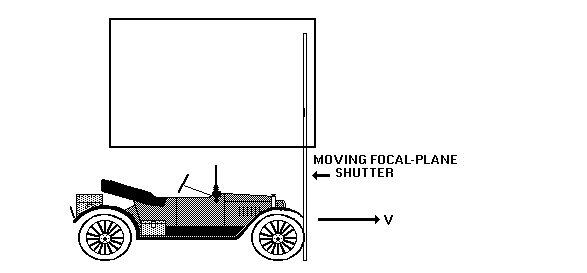
Here is the process a bit later after the car has moved a few feet and the shutter has swept a bit farther over the film:

and a bit later..

and still a bit later...
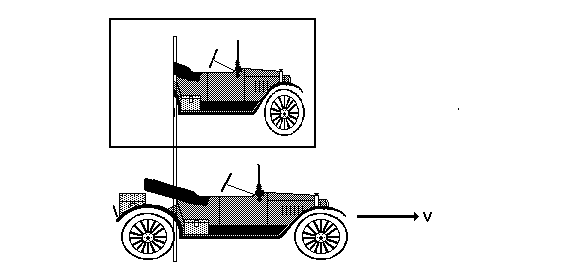
and a bit later still...
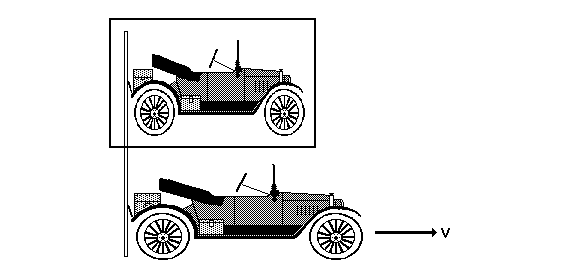
Notice how since (1) the car was moving and (2) the film was exposed with a focal-plane shutter that the image of the car is shorter than the car. Again a differing interpretation of "simultaneous" makes the image of the car contracted exactly as happens in relativity.
Suppose there were large clocks on the front of the car reading time in hundredths of a second. Suppose also that the clocks were perfectly synchronized on the car. Then in the photograph the front clock will show less time ("be behind") than the rear clock simply because it was exposed onto the film first. Again this is what happens in SR. If two clocks are synchronized in an inertial frame in which they are at rest then when they are observed from a frame in which they are moving the front clock will be behind the rear clock.
In fact, we can use the concept of the FOCAL-PLANE SHUTTER
to make a model of what happens in SR.