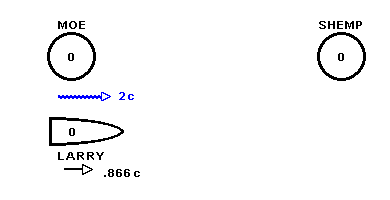
The Dog School of Mathematics Presents

11. Faster Than Light?

What about faster than light speed?  Can anything travel faster than light?  Didn't Einstein say that nothing can travel faster than light?  Well, let's look at "something" traveling faster than light and see what the consequences are.

Let's go back to our Twin-Paradox friends Moe, Larry and Shemp but this time let's suppose that as Larry leaves Moe's planet "something" also passes Moe's planet at twice the speed of light heading in the direction of Shemp's planet

The figure shows the situation in Moe's and Shemp's inertial frame. (they are each at rest with respect to the other and so are in the same inertial frame)  In this frame all clocks read 0 at the moment Larry's space ship and the "something" that is traveling at twice light speed leave Moe's planet and head toward Shemp's planet which is about 8.66 light years (1 light year = the distance that light travels in one year) away when measured in Moe's and Shemp's frame.

Here is the situation when the "something" arrives at Shemp's planet

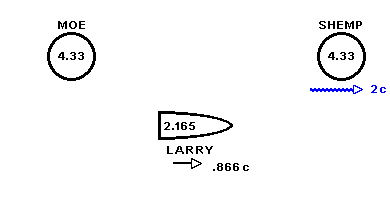
Again let me emphasize that this is all according to measurements made in Moe's and Shemp's inertial frame.  The "something" has taken 4.33 years to get from Moe's planet to Shemp's planet.  Also, since Larry's clock is running at half the speed of Moe's and Shemp's clock his clock reads half the elapsed time as theirs.  The important thing to emphasize is that Since, in Moe's and Shemp's frame, these two clocks are synchronized Moe and Shemp conclude that it took the "something" 4.33 years to travel from Moe's planet to Shemp's planet.

Now let's look at things in Larry's frame.  Larry is traveling in the same direction as the "something"  at a speed of  .866 c (again, all these measurements are in Moe's and Shemp's frame). Also recall rule (1) regarding the synchronization of moving clocks.  According to this rule if Moe's and Shemp's clocks are synchronized in their frame then they won't be synchronized in Larry's frame.  Since (in Larry's frame) Moe and Shemp are moving at .866 c toward the left in the picture it follows from rule (1) that Shemp's clock (the rear clock) will be ahead of Moe's clock.  In fact, as was shown in  8. The Twin Paradox Shemp's clock reads 7.5 years ahead of Moe's clock when they are measured in Larry's frame.  In other words, When Moe's clock reads 0 the situation (viewed in Larry's frame) is like this:

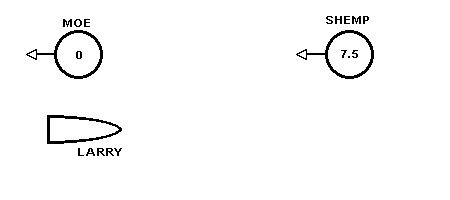
But the "something" left Moe's planet when Moe's clock read 0.  That means this "picture" shows what was happening when (in Larry's frame) the "something" was at Moe's planet.  However the something was at Shemp's planet when Shemp's clock read 4.33.  In the diagram it reads 7.5.  That means that the "something" has already been at Shemp's planet.  We can calculate how long ago (in Larry's frame) it was at Shemp's planet.  Shemp's clock showed 4.33 years elapsed time since the "something" was there.  But in Larry's frame Shemp's clock is running at one-half speed due to  time dilation .  Thus, according to Larry's clock the "something" was at Shemp's place 2 x (7.5 - 4.33) = 6.46 years ago and is just now arriving at Moe's. In Larry's frame it was at Shemp's planet 6.46 years BEFORE it was at Moe's planet.

If this "something" is in a certain class of objects then we will have our usual idea of cause and effect ruined.  If the "something" was a twice-light-speed bullet that Moe shot at Shemp then the bullet would have killed Shemp 6.46 years before it was fired by Moe.

"Your Honor, ladies and gentlemen of the jury, I submit that my client, Moe, could not be responsible for Shemp's death.  It is alleged by the prosecutor that Moe shot Shemp with his newly-invented gun that shoots bullets at twice the speed of light.  However as Larry has clearly proven here in court Shemp was killed over 6 years before Moe's gun was invented!"
If the "something" is any sort of signal that could cause any effect at Shemp's planet then if the signal was sent by Moe we would have the effect happening before it was caused.  This would throw our whole understanding of "cause and effect" upside down.  If there existed a way for a something to be sent out faster than light then in some perfectly valid inertial frame it would arrive before it was sent.

This can lead to weird paradoxes.  Suppose Shemp has a twice-light-speed gun too.  Suppose also that Shemp's policy is to return fire when and only when he is fired upon.  Suppose also that Shemp is a much better shot than Moe so that Moe's shot just missed Shemp's planet but Shemp seeing the bullet whizz by returns fire that hits the mark and destroys Moe's planet.

Then in some perfectly valid inertial frame Moe's planet would have been destroyed before Moe fired the shot that caused Shemp to destroy Moe's planet.  Since, in that frame, Moe's planet was destroyed before Moe fired the shot at Shemp Moe would have been unable to fire the shot in the first place.  Therefore Shemp would not have been shot at by Moe and would not have returned fire so Moe's planet would not have been destroyed so Moe was able to shoot at Shemp so Shemp did return fire and destroy Moe's planet so Moe didn't fire the shot so ...

paradox

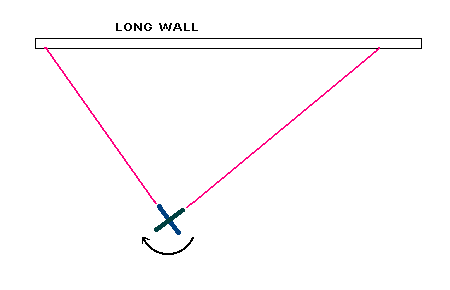
Does that mean that nothing can travel faster than light in Special Relativity?  Well, there can be many things that can travel faster than light with out transferring cause to effect.  For example imagine a powerful laser spinning on a rapidly rotating base (kind of a high tech lighthouse).  If there is a long white wall far far away from the laser and the laser projects its spot on that wall then the spot can move at much faster than the speed of light.

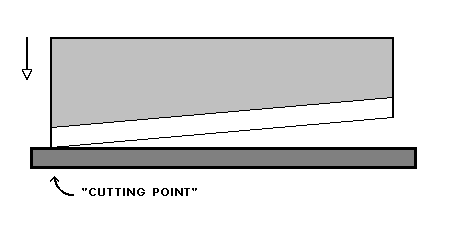
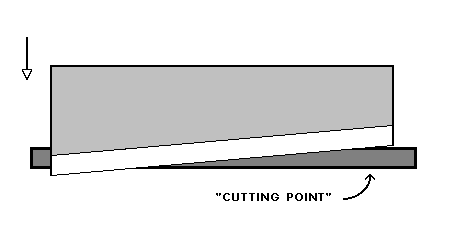
Note that if the Laser were to shine on Moe's planet and then on Shemp's planet 4.33 years later (measured in Moe's and Shemp's inertial frame--always gotta know what frame you're talking about) then Larry would observe it shining on Shemp's planet first and then Moe's planet.  Note also that Moe couldn't do anything to influence how or when the spot arrived at Shemp's planet.  Moe couldn't send any signal or information to Shemp using the spot since the spot's behavior is completely determined when the laser turns and that happens far away from Moe.

Another classic faster-than-light "something" is the giant guillotine.  It has a blade with a slightly oblique blade edge traveling downward against a stationary block.

As the blade slides down the "cutting point" where the blade edge intersects the block edge will travel to the right.

If the angle is slight it is possible for the "cutting point" to travel faster than light speed.

Here, however, there is no material object that is traveling to the right faster than light speed but just the geometric point of intersection.  Notice also that if the "cutting point" were moving to the right as pictured above at 2c in Moe's and Shemp's frame then Larry would observe it moving to the left.  The moving blade would have a different shape in Larry's frame than it did in Moe's and Shemp's frame.  How can this be?

Well, the shape of a physical object depends on exactly where its various "parts" are at any given time.  "at any given time."  Aha, there's the key!  The shape of a physical object is defined by the location of each "point" of the object simultaneously.  If the object is moving with respect to various inertial frames then observers who are in different  inertial frames will measure different "events" of the object to be simultaneous.  The result is that different observers will observe the object to have different shapes.

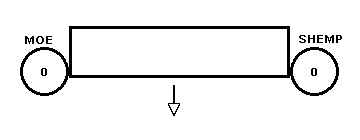
Let's see that in pictures.  Imagine a giant rectangular plate of steel moving perpendicular to the line joining Moe and Shemp.  The left end just grazes Moe's planet at the same time that the right end grazes Shemp's planet.  This means that Moe's clock reads the same when the edge of the rectangle grazes his planet as Shemp's clock does when it grazes by his.

But as we have seen, in Larry's frame Moe's and Shemp's clock read zero at different times.  Thus the Rectangular plate will be sheared when viewed in Larry's frame.  It will no longer be a nice rectangle.  In Larry's frame it will be moving downward and to the right and will appear kind of like this:
 
 
The "rectangular plate" as observed in Larry's frame

Notice that the right end is "lower" than the left end (in our picture, in space there is no up or down!).  It will come into contact with Shemp's planet before the lower left corner comes into contact with Moe's planet.  This is consistent with Larry's observation that Shemp's clocks are ahead of Moe's clocks as we saw in  8. The Twin Paradox .

This deformation is due to different configurations of space and time as measured by different observers.  It might occur that a signal could be sent from Moe to Shemp instantaneously by wiggling a long, rigid rod with one end on Moe's planet and the other end on Shemp's planet.  Kind of like a 8.66 light-year-long billiards cue stick.  When Moe wishes to communicate "instantaneously" with Shemp he just wiggles out a message in morse code.  The movements could be confined to very slow short wiggles (one centimeter per week?) so we don't have to worry about  relativistic length contraction of the stick.

But is there really such a thing as a "rigid" stick?  If it were a pipe full of air instead of a "rigid" stick and we were to move the air with a plunger or piston or some such thing, then the wiggle would travel down the air at the speed of sound.  Similarly, the disturbance in the end of the stick would travel down the stick at the speed of sound in the stick.  It would not travel faster than light.  Thus Special Relativity tells us that the concept of a completely "rigid" object leads to contradictions.

We found in  10 Addition of Velocities and Mass Increase that you couldn't reach the speed of light by just speeding up at a high rate of acceleration for a long time.  The addition of velocities formula says that after any number of such speed-ups you will still be traveling at less than the speed of light relative to the inertial frame in which you began.  Any material object or information traveling faster than light creates the concept of effects happening before their causes.  This leads to paradoxes.

Thus the problem of faster than light travel in SR is not as simple as just finding a way to go fast enough.  If SR is at least "locally" true ("locally" just as the earth is "locally" flat.) then any way to travel faster than light will call on some strange and interesting concepts.

I wonder exactly what they will be?
 

Next: 12 Relativity and the Focal-Plane Shutter

Send any comments, criticisms or reactions to:

 dogschool@dog.com