The Dog School of Mathematics presents:
SPECIAL RELATIVITY: A VIEW FROM THE KENNEL
A. IN LIEU OF A PREFACE:
These "nickel lectures" are designed to give you a feeling as to what is going on with space and time in Einstein's Special Theory of Relativity. The target audience is made up of interested students who have successfully completed the sixth grade. The level of mathematical sophistication required is very small. The main requirement is a desire to understand.
Only the kinematics of special relativity (SR) will be dealt with. "Kinematics" is a fancy word for the (usually mathematical) description of motion. Kinematics does not deal with the causes of motion. Speed position, acceleration are kinematic quantities. Force, momentum, energy etc. are under the rubric of "kinetics." We will only touch on kinetics in these lectures. Most of the "strange results" of SR are in kinematics or derive from relativistic kinematics.
I claim no originality in the items presented here. Most, if not all of it was stolen from various sources. The point of this presentation is to cut to the chase and avoid extraneous filler.
SR (0)
Special relativity was introduced in 1905 in a paper titled, "On The Electrodynamics of Moving Bodies" by Albert Einstein. Although he was led to his discoveries by problems he perceived in the classical theory of electrodynamics his theory deals with the concepts of space and time as viewed by observers moving relative to one another with uniform velocities.
The goal of the relativity lessons is to understand relativity well enough to resolve the "paradoxes" that people who don't understand it constantly post on sci.physics claiming to have found a flaw.
We begin with a (boring) derivation of the Galilean addition of velocities formula. This is the pre-relativity answer to the question:
If a railroad car is going
at velocity v relative to you and I am going
at velocity v relative to
the railroad car, how fast am I going relative
to you?
We'll answer this question in excruciating detail just to make us aware of the assumptions we use in the answer. The change from classical physics to relativity physics has to do with a slight alteration in these assumptions.
Here we go:
What is speed? It's the distance traveled divided by the elapsed time. If I travel 88 ft in one second then I'm going 88 feet per second. If I travel 176 feet in 2 seconds then I'm still going 88 feet per second. If I travel 60 miles in 3600 seconds then that's still 88 feet per second.
The other aspect of speed is that it is what I multiply times the elapsed time to get the distance traveled. If I go 45 miles per hour for 20 minutes (= 1/3 hour) then I will have traveled 15 miles. Or, as we all learned in school, d = vt
With this in mind let's work out the addition of velocities formula
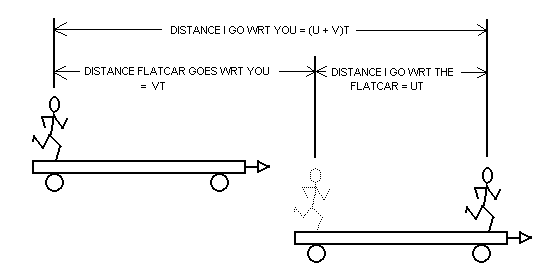
If the railroad flatcar is going at velocity v with respect to (WRT) you then after t seconds t will have moved a distance vt away from you. If I am going at velocity u with respect to the flatcar then after the same t seconds I will have moved a distance ut along the flatcar. How far have I moved away from you? Well, the flatcar has moved vt and I have moved an additional ut so the total distance I have moved is ut + vt = (u + v)t.

This can be written as (u + v)t. Now speed is the thing you multiply times time to get the distance. Here we multiply time t by (u + v) to get the distance I have traveled away from you. That means that relative to you I am traveling at the speed
speed of me relative to you = u + v
This is the formula the crackpots use when they post something like the following to sci.physics.
******* CRACKPOT_MODE = ON ************
"Einstein said that nothing can go faster than
c but if I'm in a
rocket going at 1/2 c and I shine a laser
out of the nose of my
rocket then the laser beam is going 1 1/2
c so Einstein is wrong."
******** CRACKPOT_MODE = OFF **********
The amazing thing is that the poster seems to think that for over 90 years the world's great physicists have been doing relativity and have never stumbled onto this "remarkable" argument. We'll learn later why it doesn't work.
Send any comments, criticisms or reactions to: