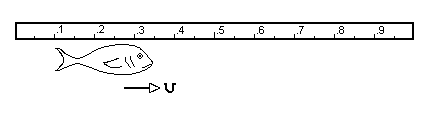
Suppose an oceanographer wished to measure the length of a fish that swims by his meter stick. He would note, at some moment, where the head was and AT THE SAME MOMENT he would notice where the tail was. The fish would then be said to be the same length as the distance between the two marks on the meter stick. If the oceanographer were to notice where the head was, wait a moment and then look where the tail was the fact that the fish was moving through the water would give a shorter measurement. Let's see that it pictures:

Look at both ends simultaneously:

head point: .35 meters
tail point: .1 meters
Length = .35 meters - .1 meters = .25 meters

Now, the "wrong" way

Look at the head first:

head point: .35 meters.

(wait a moment)

Now look at the tail:

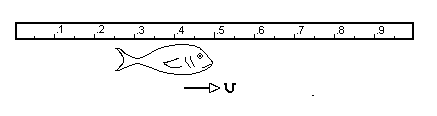
tail point: .25 meters.

length = .35 meters - .25 meters = .1 meters.

For two objects to be the same length their endpoints must coincide SIMULTANEOUSLY. The measuring process for a moving object includes the concept of simultaneity. But, as we have seen events deemed simultaneous in one inertial frame are not always simultaneous in another inertial frame. Thus the length of an object will be different when measured in different inertial frames.  Since all these inertial frames are equally valid (postulate 1) each of their measurements are as correct as any other's.

Let's go back and look at the space train incident, but this time from B's viewpoint.

We remember the events that both observers agreed happened:

• a meteor hit the right end.
• a meteor hit the left end.
• A saw both hits at the same time.
• B saw the right hit.
• B saw the left hit after seeing the right hit.

Let's consider the implication of this. A is moving to the left.  The right ends line up and are hit by a meteor. Later (after A has traveled to the left a bit) the left ends line up and are hit by another meteor. The conclusion is that A is shorter than B.

Here it is in B's frame:

Meteor hits right ends:

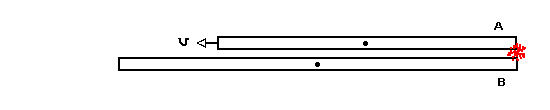
A moves to the left at 1/2 c and meteor hits left ends. It turns
out that in this example B sees the right hit at the same time as
the left hit occurs.

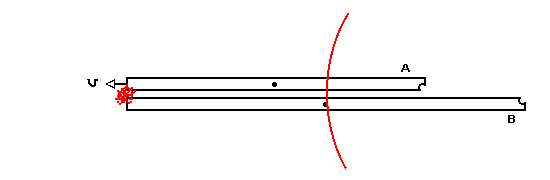
Next A, continuing to move to the left, encounters the light signal
from the left hit just as the light signal from the right hit catches
up with her.

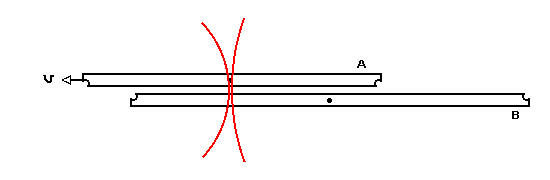
Finally B sees the light signal from the left hit.

Now we have been using the meteor hits as the events that are seen by the pilots of the space trains. However less dramatic but still equally valid events could have been the ends of the space trains coinciding. In A's frame the ends coincided simultaneously whilst in B's frame the right ends coincided first and later the left ends coincided.

Thus in A's frame the space trains are of equal length while in B's frame A's space train is shorter than B's.

[* in this example if A's and B's space trains were to end up in the same frame. B's would be longer than A's, but not by as much as is measured in the example given above. A's space train is "contracted" by its motion in B's frame to make it shorter than it would be at rest. Similarly in A's frame B is contracted by its motion such that it is the same length as A. The length of an rigid object measured in a frame in which it is at rest is called its PROPER length. If the object were to be measured in a frame in which it is moving at, say, 86.6% of c then its length would be measured in that frame as 1/2 its proper length. *]

From this example we can make two rules. Since the hits were simultaneous in A's frame but in B's frame the right hit happened before the left hit (and in B's frame A is moving to the left) we get:

RULE 1) If two events are simultaneous in an inertial frame A and
that frame has velocity v in our frame along the line from
one event to the other, then in our frame the rear event
happened before the front event.

RULE 2) If an object has length L in the frame in which it is at
rest then it as a shorter length when measured in a frame
in which it is moving along the direction of its length.

Thus it is the relativity of simultaneity that leads to relativistic length contraction. The process of measuring length relies on measuring the simultaneity of events which are separated in space. This, as we have seen, is relative. Different inertial frames measure different events as simultaneous.

"RELATIVE" AND "ABSOLUTE"

There are many quantities in our lives that are relative to our frames.  The direction of Columbus, Ohio from here depends on where "here" is.  How fast the flight attendant's cart is moving depends if you are on the ground or inside the airplane.

Relativity simply extends qualities formerly thought of as absolute (i.e. independent of frame of reference) to a new classification as relative. Since we have spent our whole lives pretty much in the same inertial frame we tend to think of things as simultaneity and length as being absolutes. It is hard to imagine them as not being absolute. This is not because of logical requirement for length or simultaneity.  It's just the prejudices we've developed over our lifetimes.

One final example: Imagine that the space trains have a row of blinking lights along the side that all flash simultaneously. If such a space train is moving by us we will see the rearward lights flash first and the more forward lights flash later. This is in accordance with RULE 1) If we plot where the flashes happened in our frame (the "points in space") then it will look like this:
 
 

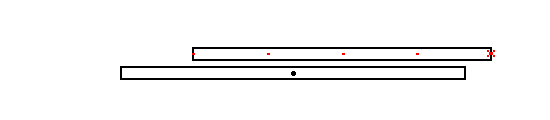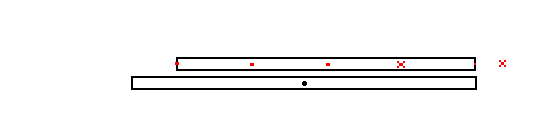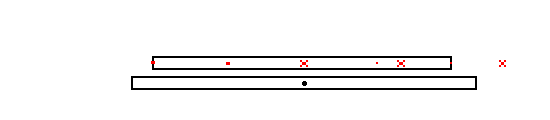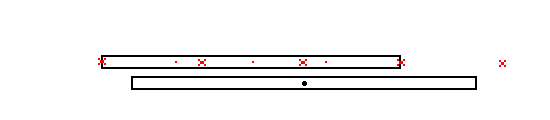Now the relativistically contracted space train flew past us.  in doing so its lights flashed. They flashed in sequence beginning with the most rearward light flashing first continuing until the front light flashed. We marked the point in space for each flash of light (in our frame). If we now look at where the flashes were AND we make the assumption that the space train that made them is AT REST then we conclude that we are shorter than it. If we assume that it is at rest (that is, it's not moving with respect to our inertial frame) Then the rearmost light is still where its flash was when the front most light flashes.  Our assumption of it being at rest in our frame means that when the front light flashes the rearmost light (simultaneously) is where its flash was observed a few moments ago.

So even we can conclude that we are shorter than the "moving" space train if we adopt its version of simultaneous.

If, however, we watch it move we will conclude that it is shorter than we are and will notice that the rearmost light has moved far away from the "point in space" where its flash was when we notice the front most light flashing.
 

 Next: 5. An Aside Concerning Language

Send any comments, criticisms or reactions to:

 dogschool@dogmail.com