In the beginning of these "lessons" I derived the Galilean Addition-of-Velocities Formula. It's the pre-relativity answer to the question:

If I'm running 10 miles per hour down the aisle of the train
and the train is going 25 miles per hour down the track then
how fast am I running when measured against the track?

Let's go back and review the derivation I used but we'll now give it a relativistic criticism:

We were answering the question:

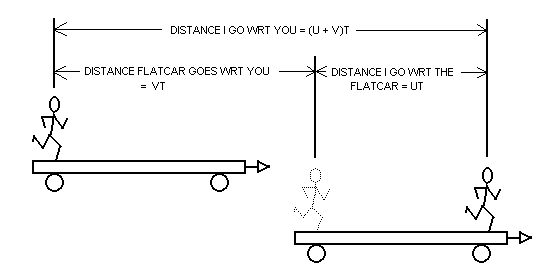
If I am going at velocity  v  relative to you and a rocket is going
at velocity  u  relative to me how fast is the rocket going relative
to you?

This can be written as (u + v)t. Now speed is the thing you multiply times time to get the distance. Here we multiply time t by (u + v) to get the distance I have traveled away from you. That means that relative to you I am traveling at the speed

       speed of me relative to you = u + v

That was our derivation way back in SR (0). We used the "normal" concepts of space and time (the ones used by Galileo and Newton) in the derivation.

Now we see some problems. The distance ut that the rocket went relative to me is not the same distance away from me when it is measured in your frame. There are at least two (three?) things to consider:

1) The distance labeled ut (measured in my frame) is contracted
because of length contraction when it is measured in your
frame.

2) The "t" in the formula ut was the elapsed time as measured
with my clocks which are

a) running slower than your clocks (when measured by you) and

b) not synchronized. When I measure the elapsed time I need to
use two different clocks. The clock where the rocket begins
and the clock where the rocket ends the timing. I observe
these two clocks as synchronized but you view them as
not synchronized.

u is my velocity measured in YOUR frame
v is the rocket's velocity measured in MY frame
w is the rocket's velocity measured in YOUR frame
c is the speed of light.

Notice that the top of the formula is simply u + v which is the "old" Galilean formula--the normal way. This is divided by (1 + uv/c²)--a sort of "fix-up factor". If u and v are small compared with the speed of light then the fraction uv/c² will be very, very close to zero and the "fix-up factor" will be very, very close to 1. That means that for speeds that we usually encounter in automobiles, jet planes, space shuttles etc. the difference between the old formula and the relativistic formula is too small to measure. When we deal with speeds comparable to the speed of light, however, the "fix-up factor" becomes significant.

Let's plug some numbers in the formula for speeds comparable to c and see how it behaves.

If I am going at .5 c relative to you and the rocket goes .5c relative to me how fast will it go relative to you? In this case both u and v are .5c and the formula gives

w = (.5c + .5c) / (1 + (.25c²)/c²)

w = .8c

What if I'm going .5c and I turn on my headlights. How fast will you see the light from my headlight going? (Note: by the second postulate this had better be c or else something's wrong!)

.w = (.5c + c)/(1 + (.5c²)/c²) = (1.5c)/(1.5) = c

There are two consequences that follow from the formula for relativistic addition of velocities.

1. You can't reach the speed of light by speeding up.

[Let's say that in our "extended language" -- If I are moving with
velocity u < c in your frame and I fire a rocket with velocity
v < c as measured in MY frame then the rocket will have velocity
w < c as measured in your frame.]

w = (xc + yc)/(1 +(xyc²)/c²) = (x + y)/(1+xy)

w = (.99c + .99c)/(1 + (.99c .99c)/c²) = (1.98c)/(1.9801)

That means that if I begin with velocity less than c as measured in your frame then by speeding up (adding a velocity) by less than c will not leave me going faster than c as measured in your frame. Also, doing this "speed up" over and over again will never get me past the speed of light.

2. "Mass Increase"

F = Ma

We can divide by a to rewrite the equation as

M = F/a

How does this enter in to relativity?

Let's posit the Standard Rocket. It has a standard mass and has a standard thrust which produces a standard acceleration for a standard time. The point is that all of these rockets are identical. Since they are identical they will all have the same final velocity after their engine is finished firing (measured relative to the inertial frame in which they began).

Now suppose that we fire off one of these rockets. It is traveling through space some speed v. (measured by us) Our assistant in a large spaceship catches up with the rocket and is "drifting" alongside the rocket with another standard rocket. He points the standard rocket in the same direction as the first rocket.

At this point both rockets are traveling with speed v measured in our frame. He ignites his standard rocket and it accelerates away from him until it has a velocity v relative to him. Now under the old Galileo/Newton addition of velocities his rocket would be going at speed 2v as measured by us. However with the relativistic formula for addition of velocities this is not the case.

Under the relativistic formula his rocket is going LESS THAN 2v when measured in our frame. This means that the standard rocket had less acceleration when it was moving with respect to us than when it was at rest with respect to us.

[Firing the engine increased its velocity from v to less than 2v. Thus the change in velocity was less than v. It didn't accelerate as much.]

So we can see that moving objects resist being speeded up more than stationary objects.

[translation: Objects which are moving in our frame resist change in velocity, when that change is measured in our frame, more than objects which are at rest in our frame.]

Since, by Newton's second law, mass is what resists acceleration we can say that the mass of the rocket has increased. When it is moving with velocity v it is more difficult to speed up than when it is at rest.

Of course in the frame of the rocket there is no mass increase. Our assistant observes the rocket speeding up to v (in his frame) just as we observed the first rocket speeding up to v in our frame.

Two of the most sacred laws of physics are

1) the conservation of energy -- the proposition that energy
can be neither created from nothing nor destroyed onto nothing.

2) The conservation of momentum -- you can't start moving without
something to push against.

E = Mc²

Send any comments, criticisms or reactions to:

dogschool@dogmail.com